Η 14η Μαρτίου δεν είναι κανονική Ημέρα π φέτος. Οι λάτρεις των μαθηματικών παντού γιορτάζουν την εκδήλωση ως Ultimate Pi Day, επειδή η ημερομηνία θα αντιστοιχεί στα πρώτα πέντε ψηφία της pi (3.1415) και όχι μόνο στις τρεις πρώτες. Αυτή η μαθηματική συρροή δεν θα έρθει ξανά για έναν αιώνα, στις 14 Μαρτίου 2115.
σχετικό περιεχόμενο
- Ο κόσμος είναι γεμάτος κύκλους
Καθορισμένος ως ο λόγος της περιφέρειας του κύκλου ως προς τη διάμετρο του, το pi ( π ) είναι τόσο υπερβατικός όσο και παράλογος αριθμός, που σημαίνει ότι δεν μπορεί ποτέ να γραφεί ως λόγος δύο ολόκληρων αριθμών και συνεχίζει επ 'αόριστον χωρίς κανένα επαναλαμβανόμενο πρότυπο. Το Pi δεν είναι ο μόνος παράλογος αριθμός - υπάρχει επίσης ο αριθμός του Euler (e) και ο χρυσός λόγος ( φ, ή phi), για παράδειγμα. Αλλά εξακολουθεί να αποτελεί πηγή γοητείας, διότι η προέλευσή της είναι εύκολο να εξηγηθεί, λέει ο Mario Livio, ένας αστροφυσικός στο Ινστιτούτο Επιστήμης του Διαστημικού Τηλεσκοπίου στο Μέριλαντ.
"Όλοι μπορούν να καταλάβουν πώς προέρχεται το pi. Όλοι οι άλλοι αριθμοί είναι πιο περίπλοκοι. Ο αριθμός phi, για παράδειγμα, περιλαμβάνει ένα συγκεκριμένο τμήμα μιας γραμμής και ο αριθμός e απαιτεί να μάθετε ποιος είναι ο λογάριθμος », λέει ο Livio, συγγραφέας του βιβλίου Είναι ο Θεός μαθηματικός;
Ένα άλλο μεγάλο μέρος της έκκλησης του pi είναι ότι έχει μια παράξενη ικανότητα για να εμφανίζεται σε μαθηματικούς τύπους, πολλά από τα οποία είναι σημαντικά για τις καθημερινές διαδικασίες από την επεξεργασία εικόνας έως την πλοήγηση GPS. Εδώ είναι μόνο μια μικρή δειγματοληψία των συνηθισμένων τύπων που περιλαμβάνουν pi:
Ο μετασχηματισμός Fourier
Ονομάστηκε για το γαλλικό μαθηματικό Jean-Baptiste Joseph Fourier, αυτό το μαθηματικό εργαλείο αποσυνθέτει ένα σήμα στις συνιστώσες του συχνότητες - μάλλον σαν το πώς μια μουσική χορδή μπορεί να αναλυθεί στις συνιστώσες του. Στην ουσία, οι μετασχηματισμοί Fourier είναι ιδανικοί για την επεξεργασία σημάτων που βασίζονται σε κύματα, όπως ο ήχος ή το φως και τα μοτίβα εύρεσης. Αυτό κάνει το Fourier να μεταμορφώσει ένα θεμελιώδες εργαλείο στον σύγχρονο ψηφιακό κόσμο.
"Έχει ονομαστεί ο πιο σημαντικός αλγόριθμος που έχει αναπτυχθεί ποτέ από την ανθρωπότητα. Τώρα που μπορεί να είναι υπερβολή, αλλά ίσως δεν είναι, "λέει ο Glen Whitney, ιδρυτής και διευθυντής του Εθνικού Μουσείου Μαθηματικών της Νέας Υόρκης. Οι μετασχηματισμοί Fourier χρησιμοποιούνται συνεχώς για να καθαρίσουν τις ψηφιακές εικόνες, να προσαρμόσουν τα αστέρια της ποπ και να βρουν απομακρυσμένους πλανήτες σε τροχιά γύρω από άλλα αστέρια. Το εργαλείο είναι επίσης ζωτικής σημασίας για τις λειτουργίες φωνής προς κείμενο που είναι πλέον συμβατές με τα smartphones. "Όταν χρησιμοποιείτε το Siri ή το Google Now, ένα από τα πρώτα βήματα είναι να φωνάξετε τη φωνή σας και να κάνετε ένα μετασχηματισμό Fourier σε αυτό ... αποδεικνύεται ότι είναι πολύ πιο εύκολο να αναγνωρίσετε τα φωνήεντα όταν κοιτάξετε τους μετασχηματισμούς Fourier από ό, αρχικά τα ίδια τα σήματα ", λέει ο Whitney.
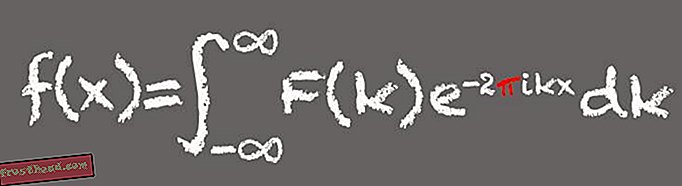(Εικονογράφηση της Victoria Jaggard) Το Pi εμφανίζεται στο μετασχηματισμό Fourier επειδή ένα από τα συστατικά μέρη ή εκφράσεις του τύπου συνδέεται με το ημίτονο και το συνημίτονο και τις γωνίες που δημιουργούνται από ένα σωματίδιο που κινείται γύρω από έναν κύκλο. "Κάθε φορά που έχετε μια φόρμουλα που ασχολείται με κύκλους ή γωνίες, δεν πρόκειται να εκπλαγείτε όταν εμφανιστεί το pi", λέει ο Whitney.
Αρχή αβεβαιότητας του Heisenberg
Ένας από τους πυλώνες της κβαντικής μηχανικής, η αρχή της αβεβαιότητας του Heisenberg δηλώνει ότι ένας παρατηρητής δεν μπορεί να γνωρίζει ταυτόχρονα τόσο τη θέση όσο και την ταχύτητα ενός υποατομικού σωματιδίου. Αντίθετα, όσο πιο συγκεκριμένα είναι γνωστή η θέση ενός σωματιδίου, τόσο λιγότερο μπορεί να είναι γνωστή η ταχύτητά του.
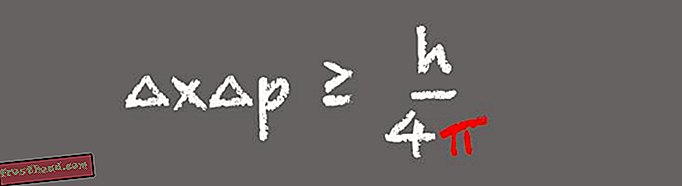(Εικονογράφηση της Victoria Jaggard) Η εμφάνιση του pi στην αρχή της αβεβαιότητας του Heisenberg έχει νόημα όταν συνειδητοποιείτε ότι στον τύπο, τη θέση και την ορμή είναι οι μετασχηματισμοί του Fourier μεταξύ τους, λέει ο Whitney. Η αρχή της αβεβαιότητας είναι σημαντική στον σύγχρονο κόσμο επειδή περιγράφει τη συμπεριφορά των σωματιδίων του φωτός ή των φωτονίων στα συστήματα επικοινωνιών οπτικών ινών. "Αυτό που μας λέει είναι ότι δεν μπορούμε να γνωρίζουμε τόσο τη θέση όσο και την ορμή των φωτονίων με εξαιρετική ακρίβεια. Δεν μπορείτε να σχεδιάσετε πρωτόκολλα επικοινωνιών που παραβιάζουν την αρχή αβεβαιότητας του Heisenberg, επειδή δεν θα λειτουργήσουν. "
Νόμου του Στόουκ
Ο νόμος του Stoke υπολογίζει τη δύναμη που απαιτείται για να μετακινήσει μια μικρή σφαίρα - δηλαδή έναν τρισδιάστατο κύκλο - μέσα από ένα ιξώδες υγρό σε μια συγκεκριμένη ταχύτητα. Έχει εφαρμογές σε πεδία που κυμαίνονται από τις επιστήμες της γης μέχρι την ιατρική.
(Εικονογράφηση της Victoria Jaggard) «Ο νόμος είναι ειδικά για την επίδραση του ιξώδους σε μια σφαίρα στο ρευστό», λέει ο Whitney, που είναι ο τρόπος με τον οποίο το pi μπαίνει στο παιχνίδι. Όσον αφορά τις πρακτικές χρήσεις του νόμου του Stoke, μην κοιτάζετε πέρα από το αυτοκίνητό σας. "Για δεκαετίες, ο τρόπος με τον οποίο οι εταιρείες σιγουρεύονται ότι το λάδι κινητήρα σας είχε το σωστό ιξώδες για το αυτοκίνητό σας ήταν να πετάξει κυριολεκτικά μια σειρά από σφαίρες δοκιμής στο πετρέλαιο και να μετρήσει το χρόνο που χρειάζεται για να πέσουν μέσα στο υγρό", λέει η Whitney. Σήμερα, ο συνηθέστερος τρόπος μέτρησης του ιξώδους του πετρελαίου περιλαμβάνει ένα εργαλείο που ονομάζεται ιξωδόμετρο τριχοειδών σωλήνων, δεν χρειάζονται σφαίρες - αλλά εξακολουθεί να αναφέρει το αποτέλεσμα σε μονάδες μέτρησης που ονομάζονται centistokes.
Φόρμουλα του Euler
Ονομάστηκε από τον ελβετικό μαθηματικό Leonard Euler, η έκδοση αυτού του τύπου που περιλαμβάνει το pi συγκεντρώνει μερικούς από τους πιο ενδιαφέροντες αριθμούς στα μαθηματικά σε ένα μέρος:
(Εικονογράφηση της Victoria Jaggard) "Όλοι πιστεύουν ότι αυτό είναι απίστευτο. Όλοι αυτοί οι αριθμοί που θεωρούμε ξεχωριστοί εμφανίζονται σε μια όμορφη εξίσωση ", λέει ο Livio. Ενώ αυτή η άθλια φόρμουλα μπορεί να εμπνεύσει δέος στους μαθηματικούς, η πιο χρήσιμη μορφή της εξίσωσης είναι ελαφρώς μεγαλύτερη:
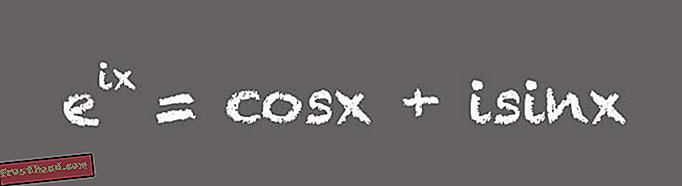(Εικονογράφηση της Victoria Jaggard) Αυτή η απελευθερωμένη έκδοση της φόρμουλας του Euler είναι ένα απίστευτο εργαλείο, λέει η Whitney. Για παράδειγμα, είναι σημαντικό για το σχεδιασμό ηλεκτρονικών συσκευών που χρησιμοποιούν εναλλασσόμενο ρεύμα ή AC. "Η φόρμουλα του Euler στην εκτεταμένη μορφή σημαίνει ότι μπορείτε να χρησιμοποιήσετε πολύπλοκες ή φανταστικές αριθμήσεις για να αναλύσετε και να σχεδιάσετε κυκλώματα AC", λέει ο Whitney. Αυτό συμβαίνει επειδή σε ένα κύκλωμα εναλλασσόμενου ρεύματος, η τάση είναι μια ποσότητα που ταλαντώνεται με την πάροδο του χρόνου - τυπικά 60 φορές ανά δευτερόλεπτο, για παράδειγμα, στην τυποποιημένη ηλεκτρική τροφοδοσία των ΗΠΑ. "Η πλήρης εκδοχή της φόρμουλας του Euler διδάσκει πώς μπορούμε να χρησιμοποιήσουμε σύνθετους αριθμούς ως μια βολική σύντομη περιγραφή για τα μοντέλα ταλαντευτικών φαινομένων", λέει ο Whitney.
Οι εξισώσεις πεδίου του Αϊνστάιν
Ένα βασικό συστατικό της γενικής θεωρίας της σχετικότητας, οι εξισώσεις πεδίου του Albert Einstein περιγράφουν πώς η βαρύτητα από τη μάζα και την ενέργεια δημιουργεί την καμπυλότητα του χωροχρόνου.
(Εικονογράφηση της Victoria Jaggard) "Περιγράφοντας ότι η καμπυλότητα περιλαμβάνει τη γεωμετρία και επειδή ο αρχικός ορισμός του pi προέρχεται από τη γεωμετρία, η εμφάνιση στην εξίσωση αυτή δεν είναι εκπληκτική" λέει ο Livio. Εκτός από την αποκάλυψη μιας θεμελιώδους αλήθειας για το πώς λειτουργεί το σύμπαν, η γενική σχετικότητα έχει πολλές πρακτικές εφαρμογές. Για παράδειγμα, οι δορυφόροι που αποτελούν το Σύστημα Παγκόσμιας Τοποθέτησης που χρησιμοποιείται για τη ναυσιπλοΐα θα ήταν απελπιστικά χωρίς συγχρονισμό μεταξύ τους, αν οι μηχανικοί δεν έλαβαν υπόψη τις επιπτώσεις της διαστολής χρόνου που προέβλεπε η θεωρία.
